Archive for October, 2020

A solution to BMO round 1 Problem 5

Posted: October 20, 2020 in Mathematics
Tags: , ,
0

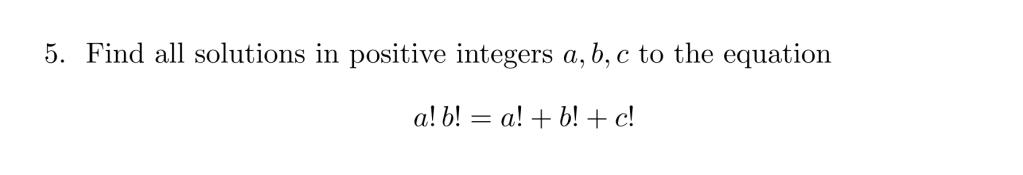
WLOG, suppose that a \leq b. Rewrite the equation as

(a!-1)(b!-1)=c!+1

Obviously, both a and b cannot be 0 or 1.

a \neq 2, otherwise if a = 2 then

b!-1=c!+1 \quad\text{or}\quad b!=c!+2

which is impossible because no two factorials have the difference of 2.

By way of contradiction, assume c \leq b, and the fact that 3 \leq a \leq b, we have

3!b! \leq a!b! = a! + b! + c! \leq 3b!

or 6 \leq 3, which is impossible. And hence b < c.

Next, we are gonna show that a = b. Assume a < b, then

a+1 \leq b \quad\text{and} \quad a+2 \leq c \quad \text{ since } a<b<c

and then

\displaystyle a!b! = a! +b! + c! \quad \text{becomes} \quad b!=1+\frac{b!}{a!}+\frac{c!}{a!}

This implies that \dfrac{b!}{a!} is odd because b! and \dfrac{c!}{a!} are both even. And this mean that

b=a+1

otherwise b \geq a+2 and \dfrac{b!}{a!} = b(b-1)\ldots(b-a-1) would be even.

So now \displaystyle b! = 1 + \frac{b!}{a!} + \frac{c!}{a!} becomes

\displaystyle (a+1)! = 1 + a+1 + \frac{c!}{a!}

\Rightarrow \quad 1 = (a+1)! - (a+1) - \dfrac{c!}{a!}

\Rightarrow \quad a+1 \mid 1 \quad\Rightarrow \quad a=0

Contradiction, and hence a = b. And so we have,

a!a!=2a!+c! \quad \text{or} \quad a! = 2+\dfrac{c!}{a!} \quad\text{for } 3 \leq a = b < c

Hence, we have

c = a + 1 \quad \text{or} \quad c = a + 2

Suppose that c \geq a + 3, then

\displaystyle 3 \mid \frac{c!}{a!} \text{ and } 3 \mid a!

then

\displaystyle 3 \mid a!-\frac{c!}{a!} = 2

Contradiction.

Case c = a + 2:

a!=2+(a+2)(a+1)=a^2+3a+4

4=a!-a^2-3a=a((a-1)!-a-3)

hence, a \mid 4 or a = 4 since a\geq 3.

Then,

4!4! = 4! + 4! + 6!

4! = 1 + 1 + 6\cdot5

24 = 32, \qquad \text{Contradiction.}

Case c = a + 1:

a!a! = a! + a! + (a+1)!

a! = 1 + 1 + a+1 = a + 3

Obviously, a = 3 and a! > a + 3 for all integer a > 3.

Therefore, (a, b, c) = (3, 3, 4) is the only solution.

One-liner Solution to IMO 2012 Problem 2

Posted: October 8, 2020 in Mathematics
Tags: , ,
0

It is not quite often that you can solve the problem from IMO in one try, but I have just found one that I can do in one line. So here is the problem 2 from IMO 2012:

And here is the Solution in one line:

\displaystyle \prod_{k=2}^n (1+a_k)^k = \prod_{k=2}^n \left(\sum_{j=1}^{k-1}\frac{1}{k-1}+a_k\right)^k \stackrel{A-G, \frac{1}{k-1}\neq a_k}{>} \prod_{k=2}^n \frac{k^k \cdot a_k}{(k-1)^{k-1}} \stackrel{\prod_2^n a_k=1}{=} n^n

Detailed explanation:

The secret ingredient of cooking this dish is to realize that you can use AM-GM inequality to pan fry those summations into products and then heat it with telescoping product to reduce the sauce to the final result you want to prove.

So, start with the (1+a_k)^k, you see there is an exponent of k, it may give us a hint that we need k terms when using AM-GM inequality, hence

\displaystyle 1+a_k = \frac{k-1}{k-1}+a_k = \frac{1}{k-1}+\frac{1}{k-1}+\cdots+\frac{1}{k-1}+a_k = \sum_{j=1}^{k-1} \frac{1}{k-1} + a_k

Next, \frac{1}{k-1} and a_k are positive, so we can apply the AM-GM inequality,

\displaystyle \frac{1}{k} \left(\sum_{j=1}^{k-1}\frac{1}{k-1} + a_k\right) \geq \left(\frac{1}{(k-1)^{k-1}} \cdot a_k\right)^{1/k}

Then raise both sides to the kth power and move the k^k to the right,

\displaystyle \left(\sum_{j=1}^{k-1} \frac{1}{k-1}+a_k\right)^k \geq \frac{k^k}{(k-1)^{k-1}} \cdot a_k

Then, multiply (n-1) of these inequalities together we get

\displaystyle \prod_{k=2}^n \left(\sum_{j=1}^{k-1}\frac{1}{k-1}+a_k\right)^k \geq \prod_{k=2}^n \frac{k^k}{(k-1)^{k-1}}\cdot a_k

Equality holds if \frac{1}{k-1}=a_k \quad \forall k \in \{2,3,\ldots,n\}, but then we have

\displaystyle \frac{1}{1}\cdot\frac{1}{2}\cdot\frac{1}{3}\cdots\frac{1}{n-1}=a_2 a_3 \cdots a_n = 1

or

(n-1)! = 1

which is impossible because by assumption n \geq 3, so this is indeed strict inequality,

\displaystyle \prod_{k=2}^n \left(\sum_{j=1}^{k-1}\frac{1}{k-1}+a_k\right)^k > \prod_{k=2}^n \frac{k^k}{(k-1)^{k-1}}\cdot a_k

or simply

\displaystyle \prod_{k=2}^n (1+a_k)^k > \prod_{k=2}^n \frac{k^k}{(k-1)^{k-1}}\cdot a_k

Then we can reduce the right side by using the telescoping product and the given assumption that a_2 a_3 \cdots a_n = 1,

\displaystyle \prod_{k=2}^n \frac{k^k}{(k-1)^{k-1}}\cdot a_k = \frac{2^2\cdot3^3\cdot4^4\cdots n^n}{1^1\cdot2^2\cdot3^3\cdots(n-1)^{n-1}}\cdot a_2 a_3 \cdots a_n = n^n

And therefore,

\displaystyle \prod_{k=2}^n (1+a_k)^k > n^n

QED